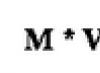Данный сервис предназначен для онлайн решения задачи оптимальной стратегии обновления оборудования . Обычно в исходных данных задаются следующие параметры:
- r(t) - стоимость продукции, произведенной в течение каждого года планового периода с помощью этого оборудования;
- u(t) - ежегодные затраты, связанные с эксплуатацией оборудования;
- s(t) - остаточная стоимость оборудования;
- р - стоимость нового оборудования, включающая расходы, связанные с установкой, наладкой, запуском оборудования и не меняющаяся в данном плановом периоде.
Планирование капитальных вложений.
Пример №1 . Найти оптимальную стратегию эксплуатации оборудования на период продолжительностью 6 лет, если годовой доход r(t) и остаточная стоимость S(t) в зависимости от возраста заданы в таблице, стоимость нового оборудования равна P = 13 , а возраст оборудования к началу эксплуатационного периода составлял 1 год.| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| r(t) | 8 | 7 | 7 | 6 | 6 | 5 | 5 |
| s(t) | 12 | 10 | 8 | 8 | 7 | 6 | 4 |
I этап. Условная оптимизация (k = 6,5,4,3,2,1).
Переменной управления на k-м шаге является логическая переменная, которая может принимать одно из двух значений: сохранить (С) или заменить (З) оборудование в начале k-го года.
1-й шаг: k = 6. Для 1-го шага возможные состояния системы t = 1,2,3,4,5,6, а функциональные уравнения имеют вид:
F 6 (t) = max(r(t), (C); S(t) - P + r(0), (З))
F 6 (1) = max(7 ; 10 - 13 + 8) = 7 (C)
F 6 (2) = max(7 ; 8 - 13 + 8) = 7 (C)
F 6 (3) = max(6 ; 8 - 13 + 8) = 6 (C)
F 6 (4) = max(6 ; 7 - 13 + 8) = 6 (C)
F 6 (5) = max(5 ; 6 - 13 + 8) = 5 (C)
F 6 (6) = max(5 ; 4 - 13 + 8) = 5 (C)
2-й шаг: k = 5. Для 2-го шага возможные состояния системы t = 1,2,3,4,5, а функциональные уравнения имеют вид:
F 5 (t) = max(r(t) + F 6 (t+1) ; S(t) - P + r(0) + F 6 (1))
F 5 (1) = max(7 + 7 ; 10 - 13 + 8 + 7) = 14 (C)
F 5 (2) = max(7 + 6 ; 8 - 13 + 8 + 7) = 13 (C)
F 5 (3) = max(6 + 6 ; 8 - 13 + 8 + 7) = 12 (C)
F 5 (4) = max(6 + 5 ; 7 - 13 + 8 + 7) = 11 (C)
F 5 (5) = max(5 + 5 ; 6 - 13 + 8 + 7) = 10 (C)
F 5 (6) = max(5 + ; 4 - 13 + 8 + 7) = 6 (З)
3-й шаг: k = 4. Для 3-го шага возможные состояния системы t = 1,2,3,4, а функциональные уравнения имеют вид:
F 4 (t) = max(r(t) + F 5 (t+1) ; S(t) - P + r(0) + F 5 (1))
F 4 (1) = max(7 + 13 ; 10 - 13 + 8 + 14) = 20 (C)
F 4 (2) = max(7 + 12 ; 8 - 13 + 8 + 14) = 19 (C)
F 4 (3) = max(6 + 11 ; 8 - 13 + 8 + 14) = 17 (C/З)
F 4 (4) = max(6 + 10 ; 7 - 13 + 8 + 14) = 16 (C/З)
F 4 (5) = max(5 + 6 ; 6 - 13 + 8 + 14) = 15 (З)
F 4 (6) = max(5 + ; 4 - 13 + 8 + 14) = 13 (З)
4-й шаг: k = 3. Для 4-го шага возможные состояния системы t = 1,2,3, а функциональные уравнения имеют вид:
F 3 (t) = max(r(t) + F 4 (t+1) ; S(t) - P + r(0) + F 4 (1))
F 3 (1) = max(7 + 19 ; 10 - 13 + 8 + 20) = 26 (C)
F 3 (2) = max(7 + 17 ; 8 - 13 + 8 + 20) = 24 (C)
F 3 (3) = max(6 + 16 ; 8 - 13 + 8 + 20) = 23 (З)
F 3 (4) = max(6 + 15 ; 7 - 13 + 8 + 20) = 22 (З)
F 3 (5) = max(5 + 13 ; 6 - 13 + 8 + 20) = 21 (З)
F 3 (6) = max(5 + ; 4 - 13 + 8 + 20) = 19 (З)
5-й шаг: k = 2. Для 5-го шага возможные состояния системы t = 1,2, а функциональные уравнения имеют вид:
F 2 (t) = max(r(t) + F 3 (t+1) ; S(t) - P + r(0) + F 3 (1))
F 2 (1) = max(7 + 24 ; 10 - 13 + 8 + 26) = 31 (C/З)
F 2 (2) = max(7 + 23 ; 8 - 13 + 8 + 26) = 30 (C)
F 2 (3) = max(6 + 22 ; 8 - 13 + 8 + 26) = 29 (З)
F 2 (4) = max(6 + 21 ; 7 - 13 + 8 + 26) = 28 (З)
F 2 (5) = max(5 + 19 ; 6 - 13 + 8 + 26) = 27 (З)
F 2 (6) = max(5 + ; 4 - 13 + 8 + 26) = 25 (З)
6-й шаг: k = 1. Для 6-го шага возможные состояния системы t = 1, а функциональные уравнения имеют вид:
F 1 (t) = max(r(t) + F 2 (t+1) ; S(t) - P + r(0) + F 2 (1))
F 1 (1) = max(7 + 30 ; 10 - 13 + 8 + 31) = 37 (C)
F 1 (2) = max(7 + 29 ; 8 - 13 + 8 + 31) = 36 (C)
F 1 (3) = max(6 + 28 ; 8 - 13 + 8 + 31) = 34 (C/З)
F 1 (4) = max(6 + 27 ; 7 - 13 + 8 + 31) = 33 (C/З)
F 1 (5) = max(5 + 25 ; 6 - 13 + 8 + 31) = 32 (З)
F 1 (6) = max(5 + ; 4 - 13 + 8 + 31) = 30 (З)
Результаты вычислений по уравнениям Беллмана F k (t) приведены в таблице, в которой k - год эксплуатации, а t - возраст оборудования.
Таблица – Матрица максимальных прибылей
| k / t | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 37 | 36 | 34 | 33 | 32 | 30 |
| 2 | 31 | 30 | 29 | 28 | 27 | 25 |
| 3 | 26 | 24 | 23 | 22 | 21 | 19 |
| 4 | 20 | 19 | 17 | 16 | 15 | 13 |
| 5 | 14 | 13 | 12 | 11 | 10 | 6 |
| 6 | 7 | 7 | 6 | 6 | 5 | 5 |
В таблице выделено значение функции, соответствующее состоянию (З) - замена оборудования.
При решении данной задачи в некоторых таблицах при оценке выбора нужного управления мы получали одинаковые значения F для обоих вариантов управления. В этом случае, в соответствии с алгоритмом решения подобных задач необходимо выбирать управление сохранения оборудования.
II этап. Безусловная оптимизация (k = 6,5,4,3,2,1).
По условию задачи возраст оборудования равен t 1 =1 годам. Плановый период N=6 лет.
К началу 1-го года эксплуатации возраст оборудования увеличится на единицу и составит: t 1 = t 0 + 1 = 0 + 1 = 1. Прибыль составит F 1 (1)=37.
Оптимальное управление при k = 1, x 1 (1) = (C), т.е. максимум дохода за годы с 1-го по 6-й достигается, если оборудование сохраняется, т.е. не заменяется.
К началу 2-го года эксплуатации возраст оборудования увеличится на единицу и составит: t 2 = t 1 + 1 = 1 + 1 = 2. Прибыль составит F 2 (2)=30.
Оптимальное управление при k = 2, x 2 (2) = (C), т.е. максимум дохода за годы с 2-го по 6-й достигается, если оборудование сохраняется, т.е. не заменяется.
К началу 3-го года эксплуатации возраст оборудования увеличится на единицу и составит: t 3 = t 2 + 1 = 2 + 1 = 3. Прибыль составит F 3 (3)=23.
Безусловное оптимальное управление при k = 3, x 3 (3)=(З), т.е. для получения максимума прибыли за оставшиеся годы необходимо в этом году провести замену оборудования.
К началу 4-го года эксплуатации возраст оборудования увеличится на единицу и составит: t 4 = t 3 + 1 = 0 + 1 = 1. Прибыль составит F 4 (1)=20.
Оптимальное управление при k = 4, x 4 (1) = (C), т.е. максимум дохода за годы с 1-го по 6-й достигается, если оборудование сохраняется, т.е. не заменяется.
К началу 5-го года эксплуатации возраст оборудования увеличится на единицу и составит: t 5 = t 4 + 1 = 1 + 1 = 2. Прибыль составит F 5 (2)=13.
Оптимальное управление при k = 5, x 5 (2) = (C), т.е. максимум дохода за годы с 2-го по 6-й достигается, если оборудование сохраняется, т.е. не заменяется.
К началу 6-го года эксплуатации возраст оборудования увеличится на единицу и составит: t 6 = t 5 + 1 = 2 + 1 = 3. Прибыль составит F 6 (3)=6.
Оптимальное управление при k = 6, x 6 (3) = (C), т.е. максимум дохода за годы с 3-го по 6-й достигается, если оборудование сохраняется, т.е. не заменяется.
F 1 (1) → (C) → F 2 (2) → (C) → F 3 (3) → (З) → F 4 (1) → (C) → F 5 (2) → (C) → F 6 (3) → (C) →
Таким образом, за 6 лет эксплуатации оборудования замену надо произвести в начале 3-го года эксплуатации
Пример №2
. Задача планирования капитальных вложений. Интервал планирования Т=5 лет. Функция затрат на ремонт и дальнейшую эксплуатацию K(t)=t+2t 2 (р.); функция замены P(t)=10+0.05t 2 (р.). Определить оптимальную стратегию замены и ремонта для нового оборудования (t=0) и оборудования возраста t=1, t=2, t=3.
Определить оптимальные планируемые затраты по годам пятилетки, если количество оборудования по возрастным группам следующие: n(t=0)=10, n(t=1)=12, n(t=2)=8, n(t=3)=5
Одной из важных экономических проблем является определение оптимальной стратегии замены старых станков, aipcraTOB и машин на новые. Старение оборудования означает его физический и моральный износ, в результате чего увеличиваются затраты на ремонт и обслуживание, возрастают производственные затраты по выпуску продукции, снижаются
производительность и ликвидная стоимость. Наступает время, когда старое оборудование выгоднее продать, заменить новым, чем эксплуатировать ценой больших затрат; причем его можно заменить новым оборудованием того же вида или новым, более совершенным. Оптимальная стратегия замены оборудования состоит в определении ее оптимальных сроков. Критерием оптимальности при этом может служить прибыль от эксплуатации оборудования, которую следует оптимизировать, или суммарные затраты на эксплуатацию в течение рассматриваемого промежутка времени, подлежащие минимизации.
Введем обозначения:
r(t) - ежегодные затраты на обслуживание оборудования возраста t лег;
g(t) - остаточная стоимость оборудования возраста t лег;
Р 0 - покупная цена оборудования.
Рассмотрим период N лет, в пределах которого требуется определить оптимальный цикл замены оборудования.
Обозначим через Л*(/) - оптимальные затраты, получаемые от
оборудования возраста t лет за оставшиеся N лет цикла использования оборудования при условии оптимальной стратегии.
Возраст оборудования отсчитывается в направлении течения процесса. Так, / = 0 соответствует случаю использования нового оборудования. На каждом этапе /V-стадийного процесса должно быть принято решение о сохранении, замене или проведении ремонта оборудования. Выбранный вариант должен обеспечивать получение минимизации суммарных затрат на эксплуатацию в течение рассматриваемого промежутка времени.
Предполагается, что переход от работы на оборудовании возраста t лег к работе на новом оборудовании совершается мгновенно, то есть замена старого оборудования и переход к работе на новом оборудовании укладываются в один период.
Пример 4.2
Оборудование эксплуатируется в течение пяти лет и после этого продается. В начале каждого года можно принять решение о сохранении оборудования или его замене новым. Стоимость нового оборудования Р 0 = 4000 руб. После t лет эксплуатации (1 g(t) = Р 0 2~‘ руб. (ликвидная стоимость). Затраты на содержание в течение года зависят от возраста оборудования t и равны r(t) = 600(/ + 1).
Определить оптимальную стратегию эксплуатации оборудования, чтобы суммарные затраты с учетом начальной покупки и заключительной продажи были минимальными.
Решение. Способ деления управления на шаги естественный - но годам, п = 5. Параметр состояния - возраст машины лу= t, ,v 0 = 0 - машина новая в начале первого года эксплуатации. Управление на каждом шаге зависит от двух переменных If и If.
Уравнения состояний зависят от управления:
Показатель эффективности А"-го шага:
(при If затраты только на эксплуатацию машины возраста t, при If машина продается (-4000 2~"), покупается новая (4000) и эксплуатируется в течение первого года (600), общие затраты равны (-4000 2 " + 4000 + 600)).
Пусть л’ (?) - условные оптимальные затраты на эксплуатацию машины, начиная с А"-го шага до конца, при условии, что к началу А"-го шага машина имеет возраст / лег. Запишем для функций Л"(г) уравнения Веллмана, заменив задачу максимизации задачей минимизации:
Величина 4000 2 0+11 - стоимость машины возраста t лет (по условию машина после пяти лет эксплуатации продается):

Из определения функций Л* (/) следует A min = Л*(0).
Представим геометрическое решение этой задачи. Отложим по оси абсцисс номер шага к, а по оси ординат - возраст машины /. Точка (к - 1, /) на плоскости соответствует началу А - -го года эксплуатации машины возраста / лет. Перемещение на графике в зависимости от принятого управления на /о-м шаге показано на рис. 4.3.

Рис. 4.3
Состояние начала эксплуатации машины соответствует точке,v‘(0, 0), конец - точкам.5(5,/). Любая траектория, переводящая точку ДА-1, /) из в.5, состоит из отрезков - шагов, соответствующих годам эксплуатации. Необходимо выбрать такую траекторию, при которой затраты на эксплуатацию машины окажутся минимальными.
Над каждым отрезком, соединяющим точки (А’ - 1, /) и (А, / + 1), записываются соответствующие управлению If затраты (600(/ + 1)), а над отрезком, соединяющим точки (к - 1, /) и (к , /), - затраты, соответствующие управлению If (4600 - 4000 2 "). Таким образом размещаются все отрезки, соединяющие точки на 1рафикс, соответствующие переходам из любого состояния лд_| в состояние s k (см. рис. 4.3).
Далее на размеченном фафе производится условная оптимизация. В состояниях (5, /) машина продается, условный оптимальный доход от продажи равен 4000 2~‘, но поскольку целевая функция связана с затратами, то в кружках точек (5, /) ставится величина дохода со знаком минус. Далее на последующих этапах выбираются минимальные затраты среди двух возможных переходов, записываются в кружок данной точки, а соответствующие управления на этом шаге помечаются пунктирной стрелкой. При этом на каждом шаге трафически решаются уравнения Веллмана (рис. 4.4).
После проведения условной оптимизации получим в точке (0, 0) минимальные затраты на эксплуатацию машины в тсченШ пяти лет с последующей продажей: A min = 11 900. Далее строится оптимальная траектория, перемещаясь из точки So(0, 0) по пунктирным стрелкам в.?. Получаем набор точек: {(0, 0), (1, 1), (2, 2), (3, 1), (4, 2), (5, 3)}, который соответствует оптимальному управлению U"(u c , U‘, U U c , U c). Оптимальный режим
эксплуатации состоит в том, чтобы заменить машину новой в начале третьего года.
Таким образом, размеченный график (сеть) позволяет наглядно интерпретировать расчетную схему и решить задачу методом динамического программирования.
Модели и вычислительные процедуры динамического программирования очень гибки в смысле возможностей включения различных модификаций задачи. Например, аналогичная задача может быть рассмотрена для большого числа вариантов управления, «ремонт», «капитальный ремонт» и г.д. Все эти факторы могут быть учтены вычислительной схемой динамического программирования.
Известно, что оборудование со временем изнашивается, стареет физически и морально. В процессе эксплуатации, как правило, падает его производительность и растут эксплуатационные расходы на текущий ремонт. Со временем возникает необходимость замены оборудования, так как его дальнейшая эксплуатация обходится дороже, чем ремонт. Отсюда задача о замене может быть сформулирована так. В процессе работы оборудование дает ежегодно прибыль, требует эксплуатационных затрат и имеет остаточную стоимость. Эти характеристики зависят от возраста оборудования. В любом году оборудование можно сохранить, продать по остаточной цене и приобрести новое. В случае сохранения оборудования возрастают эксплуатационные расходы и снижается производительность. При замене нужны значительные дополнительные капитальные вложения. Задача состоит в определении оптимальной стратегии замен в плановом периоде, с тем чтобы суммарная прибыль за этот период была максимальной.
Для количественной формулировки задачи введем следующие обозначения: r(t) - стоимость продукции, производимой за год на единице оборудования возраста t лет; u(t) - расходы, связанные с эксплуатацией этого оборудования; s(t) - остаточная стоимость оборудования возраста t лет; р - покупная цена оборудования; Т - продолжительность планового периода; t = 0,1, 2,... , Т - номер текущего года.
Решение. Чтобы решить задачу, применим принцип оптимальности Р. Беллмана. Рассмотрим интервалы (годы) планового периода в последовательности от конца к началу. Введем функцию условно-оптимальных значений функции цели Fk(t). Эта функция показывает максимальную прибыль, получаемую от оборудования возраста t лет за последние к лет планового периода. Здесь возраст оборудования рассматривается в направлении естественного хода времени. Например, t = 0 соответствует использованию совершенно нового оборудования. Временные же шаги процесса нумеруются в обратном порядке. Например, при к = 1 рассматривается последний год планового периода, при к = 2 - последние два года и т. д., при к = Т - последние Т лет, т. е. весь плановый период. Направления изменения t и к показаны на рисунке.
В этой задаче систему составляет оборудование. Ее состояние характеризуется возрастом. Вектор управления - это решение в момент t = = 0,1, 2,... , Т о сохранении или замене оборудования. Для нахождения оптимальной политики замен следует проанализировать, согласно принципу оптимальности, процесс от конца к началу. Для этого сделаем предположение о состоянии оборудования на начало последнего года (k = 1). Пусть оборудование имеет возраст t лет. В начале Т-го года имеются две возможности: 1) сохранить оборудование на Т-й год, тогда прибыль за последний год составит r(t) - u(t); 2) продать оборудование по остаточной стоимости и купить новое, тогда прибыль за последний год будет равна s(t) - р + г(0) - u(0), где г(0) - стоимость продукции, выпущенной на новом оборудовании за первый год его ввода; u(0) - эксплуатационные расходы в этом году. Здесь целесообразно разворачивать процесс от конца к началу. Для последнего года (к = 1) оптимальной политикой с точки зрения всего процесса будет политика, обеспечивающая максимальную прибыль только за последний год. Учитывая значение прибыли при различном образе действия (замена - сохранение), приходим к выводу, что решение о замене оборудования возраста t лет следует принять в случае, когда прибыль от нового оборудования на последнем периоде больше, чем от старого, т.е. при условии
Итак, для последнего, года оптимальная политика и максимальная прибыль F 1 {t) находятся из условия
Пусть к = 2, т. е. рассмотрим прибыль за два последних года. Делаем предположение о возможном состоянии t оборудования на начало предпоследнего года. Если в начале этого года принять решение о сохранении оборудования, то к концу года будет получена прибыль r(t) - u(t). На начало последнего года оборудование перейдет в состояние t + 1, и при оптимальной политике в последнем году оно принесет прибыль, равную F 1 (t + 1). Таким образом, общая прибыль за два года составит r(t) - u(t) + F 1 (t + 1). Если же в начале предпоследнего года будет принято решение о замене оборудования, то прибыль за предпоследний год составит s(t)-p+r(0)-u(0). Поскольку приобретено новое оборудование, на начало последнего года оно будет в состоянии t = 1. Следовательно, общая прибыль за последние два года при оптимальной политике в последнем году составит
Условно-оптимальной в последние два года будет политика, доставляющая максимальную прибыль:
Аналогично находим выражения для условно-оптимальной прибыли за три последних года, четыре и т. д. Общее функциональное уравнение примет вид

Таким образом, разворачивая весь процесс от конца к началу, получаем, что максимальная прибыль за плановый период Т составит F T (t 0). Так как начальное состояние to известно, из выражения для F T (t 0) находим оптимальное решение в начале первого года, потом вытекающее оптимальное решение для второго года и т.д. Обратимся к числовому примеру.
Разработать оптимальную политику замены оборудования при условиях:
1) стоимость r(t) продукции, производимой с использованием оборудования за год, и расходы u(t), связанные с эксплуатацией оборудования, заданы таблицей;
2) ликвидационная стоимость машины не зависит от ее возраста и равна 2;
3) цена нового оборудования со временем не меняется и равна 15;
4) продолжительность планового периода 12 лет.
Итак, s(t) = 2, р = 15, Т = 12.

Запишем функциональные уравнения для F 1 (t) и F к (t) при числовых значениях нашего примера:

Пользуясь выражениями (8.9), (8.10), будем последовательно вычислять значения максимальной прибыли F к (t) и записывать их в специальную таблицу (табл. 8.4). Первую строку получим, придавая параметру t в равенстве (8.9) значения 0,1,... ,12 и используя исходные данные табл. 8.3. Например, при t = 0

Заметим, что если прибыль от нового оборудования равна прибыли от старого, то старое лучше сохранить еще на год:


Из табл. 8.3 видно, что r(t) – u(t) с ростом t убывает. Поэтому при t > 9 оптимальной будет политика замены оборудования. Чтобы различать, в результате какой политики получается условно-оптимальное значение прибыли, будем эти значения (до t = 9 включительно оптимальной является политика сохранения) разграничивать жирной линией. Для заполнения второй строки табл. 8.4 используем формулу (8.10). Для к = 2 получаем

Придадим параметру t значения 0,1,2,... ,12, значения r(t) и u(t) возьмем из табл. 8.3, а значения F 1 (t + 1) - из первой строки табл. 8.4. Для третьей строки расчетную формулу получим из равенства (8.10) при к = 3:

и т. д. Заполнив табл. 8.4, данные ее используем для решения поставленной задачи. Эта таблица содержит много ценной информации и позволяет решать все семейство задач, в которое мы погружали исходную задачу.
Пусть, например, в начале планового периода имеем оборудование возраста 6 лет. Разработаем "политику замен" на двенадцатилетний период, доставляющую максимальную прибыль. Информация для этого имеется в табл. 8.4. Максимальная прибыль, которую можно получить за 12 лет при условии, что вначале имелось оборудование возраста 6 лет, находится в табл. 8.4 на пересечении столбца t = 6 и строки F12(t); она составляет 180 единиц.
Значение максимальной прибыли F12(6) = 180 записано справа от ломаной линии, т.е. в области "политики замены". Это значит, что для достижения в течение 12 лет максимальной прибыли в начале первого года оборудование надо заменить. В течение первого года новое оборудование постареет на год, т.е., заменив оборудование и проработав на нем 1 год, мы за 11 лет до конца планового периода будем иметь оборудование возраста 1 год. Из табл. 8.4 берем F11(l) = 173. Это значение располагается в области "политики сохранения", т. е. во втором году планового периода надо сохранить оборудование возраста 1 год, и, проработав на нем год, за 10 лет до конца планового периода будем иметь оборудование возраста 2 года.
Выясняем, что значение F10(2) = 153 помещено в области сохранения. Работаем на оборудовании еще год. Теперь до конца планового периода осталось 9 лет, а возраст оборудования составляет 3 года. Находим F9(3) = 136. Это область сохранения. Работаем на оборудовании еще год. Его возраст становится равным 4 годам. До конца планового периода остается 8 лет. Определяем F8(4) = 120. Это область замен. Заменяем оборудование на новое. Проработаем на нем в течение четвертого года. Оно постареет на год. До конца планового периода останется 7 лет. Находим F7(l) = 113. Это область сохранения. Продолжив подобные рассуждения, установим, что F6(2) = 93, F5(3) = 76 расположены в области сохранения, F4(4)=60 - в области замен, F3(l) = 53, F2(2) = 33, F1(3) = 16 - в области сохранения. Разработанную политику изобразим следующей цепочкой:

Таким образом, вместо поиска оптимальной "политики замен" на плановый период в 12 лет мы погрузили исходную задачу в семейство подобных, когда период меняется от 1 до 12. Решение ведется по принципу оптимальности для любого состояния системы, независимо от ее предыстории. Оптимальная "политика замен" является оптимальной на оставшееся число лет. Табл. 8.4 содержит информацию для решения и других задач. Из нее можно найти оптимальную стратегию замены оборудования с любым начальным состоянием от 0 до 12 лет и на любой плановый период, не превосходящий 12 лет. Например, найдем "политику замен" на плановый период в 10 лет, если вначале имелось оборудование пятилетнего возраста:

Задачу о замене оборудования мы упростили. На практике же деталями не пренебрегают. Легко учесть, например, случай, когда остаточная стоимость оборудования s(t) зависит от времени. Может быть принято решение о замене оборудования не новым, а уже проработавшим некоторое время. Не составляет также труда учесть возможность капитального ремонта старого оборудования. При этом в понятие "состояние" системы необходимо включить время последнего ремонта оборудования. Функция Fk(ti,t2) выражает прибыль за последние к лет планового периода при условии, что вначале имелось оборудование возраста t1, прошедшее капитальный ремонт после t2 лет службы. Характеристики г, s и и также будут функциями двух переменных t1 и t2.
Динамическое программирование. Задача о замене оборудования
Найти оптимальные сроки замены оборудования. Первоначальная стоимость оборудования q 0 =6000 усл. ед., ликвидационная стоимость L(t)=q 0 2 -i , стоимость содержания оборудования возраста i лет в течение 1 года S(t)=0,1q 0 (t+1), срок эксплуатации оборудования 5 лет. В конце срока эксплуатации оборудование продается. Задачу решить графически.
Для построения графика в ПП Wolfram Mathematica 6.0 вводим
g = Plot[{6000*2^-x, 600*(x + 1)}, {x, 0, 5}]
В итоге получаем график:
Из графика видим, что оптимальный срок замены оборудования является второй год его эксплуатации.
Динамическое программирование. Оптимальное распределение средств между предприятиями
Найти оптимальное распределение средств в размере 9 усл. ед. между четырьмя предприятиями. Прибыль от каждого предприятия является функцией от вложенных в него средств и представлена таблицей:
|
Вложенные средства |
|||||||||
|
I предприятие |
|||||||||
|
II предприятие |
|||||||||
|
III предприятие |
|||||||||
|
IV предприятие |
Вложения в каждое предприятия кратны 1 усл. ед.
Разобьем процесс выделения средств предприятиям на 4 этапа: на первом этапе выделяется y 1 средств предприятию П 1 , на втором -y 2 средств предприятию П 2 , на третьем - y 3 средств предприятию П 3 , на четвертом третьем - y 4 средств предприятию П 4
x n = x n - 1 - y n , n = 1,2,3, 4.
Заметим, что на четвертом этапе выделения средств весь остаток x 3 вкладывается в предприятие П 4 , поэтому y 3 = x 4 .
Воспользуемся уравнениями Беллмана для N = 4.
В результате получим следующие таблицы:
Таблица 1
 |
||||||||||||
Таблица 2
Таблица 3
Таблица 4
Из Таблицы 4 вытекает, что оптимальным управлением будет y 1 * =3, при этом оптимальная прибыль равна 42. Далее получаем
х 1 =х 0 -у 1 *=9-3=6, 2 (х 1)= 2 (6)=30, y 2 * =1
х 2 =х 1 -у 2 *=6-1=5, 3 (х 2)= 3 (5)=23, y 3 * =1
х 3 =х 2 -у 3 *=5-1=4, 4 (х 3)= 4 (4)=15, y 3 * =4
Таким образом, наиболее оптимальным является вложение в предприятия П1, П2, П3 и П4 денежных средств в размере 4, 1,1 и 3 усл.ед., соответственно. В этом случае прибыль будет максимальной и составит 42 усл. ед.
После того как выполнены пункты 1-7, и математическая модель составлена, приступают к ее расчету.
Основные этапы решения задачи динамического программирования:
- 1. Определение множества возможных состояний Sm для последнего шага.
- 2. Проведение условной оптимизации для каждого состояния s€ Sm на последнем m-м шаге по формуле (1.3) и определение условного оптимального управления x(s), s€ Sm
- 3. Определение множества возможных состояний Si для i-го шага, i=2,3…,m-1.
- 4. Проведение условной оптимизации i-го шага, i=2,3…,m-1 для каждого состояния s€ S m по формуле (1.4) и определение условного оптимального управления x i (s), s€ S m , i=2,3…,m-1.
- 5. Определение начального состояния системы s 1 , оптимального выигрыша W1(S1) и оптимального управления x1(S1) по формуле (1.4) при i=1. Это есть оптимальный выигрыш для всей задачи W* =W 1 (x 1 *).
- 6. Проведение безусловной оптимизации управления. Для проведения безусловной оптимизации необходимо найденное на первом шаге оптимальное управление x 1 *=x 1 (s 1) подставить в формулу (1.2) и определить следующее состояние системы s 1 =f 1 (s 1 ,x 1). Для измененного состояния найти оптимальное управление x 2 *=x 2 (s 2), подставить в формулу (1.2) и т.д. Для i-го состояния s 1 найти s i+1 =f i+1 (s i ,x i *) и x* i+1 (s i+1) и т.д.
Динамическое программирование обычно придерживается двух подходов к решению задач:
- · нисходящее динамическое программирование: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений часто встречающихся подзадач;
- · восходящее динамическое программирование: все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи.
Этот способ лучше нисходящего программирования в смысле размера необходимого стека и количества вызова функций, но иногда бывает нелегко заранее выяснить, решение каких подзадач нам потребуется в дальнейшем.
Задача о замене оборудования состоит в определении оптимальных сроков замены старого оборудования. Критерием оптимальности являются либо доход от эксплуатации оборудования (задача максимизации), либо суммарные затраты на эксплуатацию (задача минимизации) в течение планируемого периода. Мы будем рассматривать задачу максимизации, и критерием оптимальности будет доход от эксплуатации оборудования.
Принцип оптимальности Беллмана -- важнейшее положение динамического программирования, которое гласит: оптимальное поведение в задачах динамического программирования обладает тем свойством, что каковы бы ни были первоначальное состояние и решение (т. е. “управление”), последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения. Этот принцип можно выразить и рассуждая от противного: если не использовать наилучшим образом то, чем мы располагаем сейчас, то и в дальнейшем не удастся наилучшим образом распорядиться тем, что мы могли бы иметь.
Следовательно, если имеется оптимальная траектория, то и любой ее участок представляет собой оптимальную траекторию.
Этот принцип позволяет сформулировать эффективный метод решения широкого класса многошаговых задач.
Под функцией Беллмана в текущий момент времени понимаем минимальное значение критерия качества в текущий момент времени: Если t=0, то
Таким образом, значение функции Беллмана S(x,t) определяет минимальную величину функционала для любого начального состояния x(t) в любой момент времени t . С другой стороны, значение функции Беллмана совпадает со значением, так называемых текущих потерь на управление:
Эксплуатация оборудования планируется в течение n лет, но оборудование имеет тенденцию с течением времени стареть и приносить все меньшую годовую прибыль r(t) , где t - возраст оборудования. При этом есть выбор: либо в начале любого года продать устаревшее оборудование за цену S(t) , которая также зависит от возраста, и купить новое оборудование за цену P , либо оставить оборудование в эксплуатации. Требуется найти оптимальный план замены оборудования с тем, чтобы суммарная прибыль за все n лет была максимальной, учитывая, что к началу эксплуатационного периода возраст оборудования составляет t 0 лет.
Входными данными к этой задаче являются:
r(t) - доход от эксплуатации в течение одного года оборудования возраста t лет;
S(t) - остаточная стоимость оборудования;
P - цена нового оборудования;
t 0 - начальный возраст оборудования.
Переменной управления на k -м шаге является логическая переменная, которая может принимать два значения: С - сохранить , З - заменить оборудование в начале k -го года. Переменной состояния системы на k -м шаге является переменная t .
Функцию Беллмана F k (t) определим как максимально возможную прибыль от эксплуатации оборудования за годы с k -го по n -й, если к началу k -го года возраст оборудования составлял t лет. Применяя то или иное управление, мы переводим систему в некоторое новое состояние, а именно, если в начале k -го года мы оборудование сохраняем, то к началу следующего (k+1) -го года его возраст увеличится на 1 (состояние системы станет равно t +1), за год оно принесет прибыль r(t) , и максимально возможная прибыль за оставшиеся годы (с (k+1) -го по n -й) составит F k+1 (t+1) . Если же в начале k -го года принимаем решение на замену оборудования, то мы продаем старое оборудование возраста t лет за цену S(t) , покупаем новое оборудование за цену P и эксплуатируем его в течение k -го года, что приносит за этот год прибыль r(0) . К началу следующего года возраст оборудования составит 1 год, и за все годы с (k+1) -го по n -й максимально возможная прибыль будет F k+1 (1) .
Из этих двух вариантов управления выбираем тот, который приносит большую прибыль. Уравнение Беллмана на каждом шаге имеет вид:
Функцию Беллмана для первого шага (k=n ) легко вычислить - это максимально возможная прибыль только за последний n -й год:

Вычислив значение функции F n (t) по формуле (2), далее можно посчитать F n-1 (t) , затем F n-2 (t) и так далее до F 1 (t 0 ) . Функция F 1 (t 0 ) представляет собой максимально возможную прибыль за все годы (с 1-го по n -й). Этот максимум достигается при некотором управлении, применяя которое в течение первого года, мы определяем возраст оборудования к началу второго года (в зависимости от того, какое управление является для первого года оптимальным, это будет 1 или t 0 +1). Для данного возраста оборудования по результатам, полученным на этапе условной оптимизации , мы смотрим, при каком управлении достигается максимум прибыли за годы со 2-го по n -й и так далее. На этапе безусловной оптимизации отыскиваются годы, в начале которых следует произвести замену оборудования.